Funkcja kwadratowa

f

jest określona wzorem

f(x)=a(x-1)(x-3)

. Na rysunku przedstawiono fragment paraboli będącej wykres tej funkcji. Wierzchołkiem tej paraboli jest punkt

W=(2,1)

. Osią symetrii paraboli będącej wykresem funkcji

f

jest prosta o równaniu

ODPOWIEDŹ A: $x = 1$

ODPOWIEDŹ B: $x = 2$

ODPOWIEDŹ C: $y = 1$

ODPOWIEDŹ D: $y = 2$

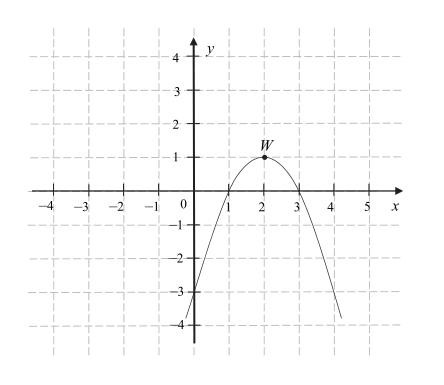
Krok 1: Wyznaczenie osi symetrii paraboli

Dla funkcji kwadratowej w postaci iloczynowej $f(x) = a(x-x_1)(x-x_2)$ , oś symetrii paraboli przechodzi przez środek między miejscami zerowymi:

x = \frac{x_1 + x_2}{2}

W naszym przypadku miejsca zerowe to $x_1 = 1$ i $x_2 = 3$ , więc:

x = \frac{1 + 3}{2} = 2

Krok 2: Potwierdzenie przez współrzędne wierzchołka

Wierzchołek paraboli $W = (2, 1)$ leży na osi symetrii, co potwierdza, że oś symetrii to:

x = 2

Osią symetrii paraboli jest prosta $x = 2$ (odpowiedź B).