Dwa stożki o takich samych podstawach połączono podstawami w taki sposób jak na rysunku. Stosunek wysokości tych stożków jest równy

3 : 2

. Objętość stożka o krótszej wysokości jest równa

12\ \text{cm}^3

. Objętość bryły utworzonej z połączonych stożków jest równa

ODPOWIEDŹ A: $20\ \text{cm}^3$

ODPOWIEDŹ B: $30\ \text{cm}^3$

ODPOWIEDŹ C: $39\ \text{cm}^3$

ODPOWIEDŹ D: $52,5\ \text{cm}^3$

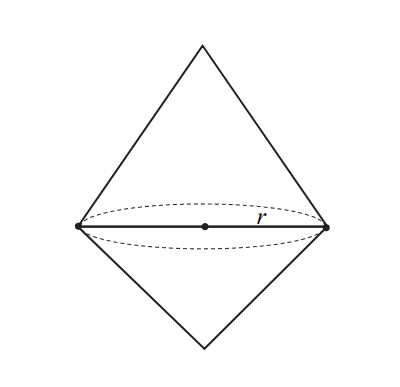
Krok 1: Ustalenie stosunku wysokości i objętości

Mamy dwa stożki o tym samym promieniu podstawy $r$ i różnych wysokościach. Stosunek wysokości wynosi:

h_1 : h_2 = 3 : 2

Objętość stożka o krótszej wysokości $h_2$ wynosi $V_2 = 12\ \text{cm}^3$ .

Krok 2: Obliczenie objętości drugiego stożka

Objętość stożka wyraża się wzorem:

V = \frac{1}{3}\pi r^2 h

Ponieważ stożki mają tę samą podstawę, stosunek ich objętości jest równy stosunkowi ich wysokości:

\frac{V_1}{V_2} = \frac{h_1}{h_2} = \frac{3}{2}

Obliczamy objętość większego stożka:

V_1 = \frac{3}{2} \times V_2 = \frac{3}{2} \times 12\ \text{cm}^3 = 18\ \text{cm}^3

Bryła składa się z obu stożków połączonych podstawami, więc jej objętość to suma objętości:

V_{\text{całkowita}} = V_1 + V_2 = 18\ \text{cm}^3 + 12\ \text{cm}^3 = 30\ \text{cm}^3

Objętość bryły wynosi $30\ \text{cm}^3$ (odpowiedź B).